Introducción a la programación de computadoras#
Una computadora es una máquina que ejecuta automáticamente secuencias de instrucciones llamadas programas. La programabilidad de las computadoras permite que su funcionamiento pueda modificarse sin alterar sus componentes físicos, lo que posibilita que ayuden a resolver una gran variedad de problemas y las hace mucho más versátiles que otros tipos de máquinas.
Las computadoras trabajan con un modelo de Entrada - Procesamiento - Salida: reciben datos de entrada (ej. números), los procesan (ej. realizan cálculos aritméticos) y generan salidas (resultados de los cálculos).
La gran mayoría de las computadoras modernas son electrónicas y digitales. Utilizan circuitos integrados para procesar y almacenar información en forma de señales eléctricas. Esta representación de la información se basa en el sistema binario, utilizando solo dos estados: 0 (voltaje bajo) y 1 (voltaje alto).
En el nivel más básico, las computadoras pueden programarse introduciendo directamente combinaciones de unos y ceros, conocidas como lenguaje máquina. Ya que esta forma de programación es poco amigable para los seres humanos, es más usual utilizar lenguajes de programación de alto nivel, los cuales usan instrucciones compuestas por expresiones y palabras similares al idioma inglés.
Para utilizar una computadora en la resolución de un problema, este debe ser expresado mediante un lenguaje de programación. El pensamiento computacional es un enfoque para la resolución de problemas basado en conceptos y métodos de las ciencias de la computación que consta de cuatro principios fundamentales: descomposición, reconocimiento de patrones, abstracción y algoritmos.
Modelo Entrada - Procesamiento - Salida#
El modelo de “Entrada - Procesamiento - Salida” es un concepto fundamental en análisis de sistemas de información y desarrollo de programas. Su esquema se presenta en la Fig. 1.

Fig. 1 Modelo Entrada - Procesamiento - Salida.#
La entrada se refiere a los datos que se introducen en un sistema o programa para ser procesados. Pueden ingresarse a través de diversas fuentes, tales como teclados, ratones, cámaras, sensores, archivos y servicios web, entre otros. El procesamiento es el conjunto de instrucciones que generan salidas a partir de las entradas. Estas intrucciones pueden incluir cálculos matemáticos, operaciones lógicas y operaciones de control, entre muchas posibilidades. Por último, la salida es el resultado del procesamiento (ej. el resultado de cálculos aritméticos).
Ejemplo#
El índice de masa corporal (IMC) clasifica el peso de una persona en categorías como bajo, normal y sobrepeso. Se calcula dividiendo la masa entre el cuadrado de la estatura.
De acuerdo con el modelo de Entrada - Procesamiento - Salida, el cálculo del IMC puede representarse de la siguiente manera.
Entradas
masa (kg)
estatura (m)
Procesamiento
masa/estatura^2
Salida
IMC calculado
Ejercicio
Calcule manualmente su IMC y verifique el resultado con esta calculadora. Identifique en la calculadora los elementos correspondientes a entrada, procesamiento y salida.
Historia de la computadora#
Primeras máquinas de cálculo#
Varias máquinas diseñadas para realizar cálculos aritméticos podrían considerarse precursoras de las computadoras modernas. Por ejemplo, en el siglo XVII, se construyeron varias calculadoras mecánicas capaces de sumar, restar, multiplicar y dividir.
Alrededor de 1642, el matemático francés Blaise Pascal (1623-1662) diseñó y construyó la primera calculadora de la que existe constancia, llamada la Pascalina. La creó para ayudar a su padre, que era un recaudador de impuestos, en las tareas de cálculo. La Pascalina podía realizar sumas y restas. Su tamaño y formas eran similares a los de una caja de zapatos y su funcionamiento se basaba en un conjunto de ruedas dentadas conectadas entre sí. Una característica notable de la Pascalina era su capacidad para manejar el acarreo, es decir, si al sumar un dígito el resultado era 10 o más, la máquina automáticamente añadía 1 a la siguiente rueda, que representaba la siguiente posición decimal.
La Pascalina tenía varias limitaciones y no era completamente fiable. Sin embargo, marcó un importante precedente en el desarrollo de dispositivos de cálculo automáticos.
Cerca de 1672, el matemático alemán Gottfried Leibniz (1646-1716) extendió las ideas de Pascal y creó un dispositivo llamado Stepped Reckoner o “Máquina de Leibniz” el cual, además de sumar y restar, podía multiplicar y dividir. Leibniz afirmaba que el trabajo manual de los cálculos podía relegarse en las máquinas, liberando así las capacidades de las personas para tareas de orden superior. Una réplica de la máquina de Leibniz se muestra en la Fig. 2.

Fig. 2 Réplica de la Stepped Reckoner, en el Museo Technische Sammlungen, en Dresden, Alemania. Imagen compartida a través de Wikimedia Commons.#
La innovación clave de la máquina de Leibniz fue un cilindro rotativo, llamado “Rueda de Leibniz”, con una serie de dientes de diferentes longitudes. Al girar el cilindro, estos dientes engranaban con un engranaje de conteo, moviéndolo un número variable de posiciones dependiendo de la longitud del diente que entrara en contacto con el engranaje. La suma y la resta se lograban mediante giros directos del mecanismo escalonado. La multiplicación y la división se realizaban a través de repetidas sumas y restas, respectivamente. El usuario introducía números usando un conjunto de dígitos deslizables y luego giraba una manivela para realizar cálculos. Los resultados se mostraban en una serie de ventanas en la parte superior de la máquina.
Aunque la máquina de Leibniz representó un avance significativo en la tecnología de cálculo mecánico, tenía limitaciones en cuanto a su fiabilidad y precisión en ciertas operaciones. Sin embargo, la rueda de Leibniz se utilizó en calculadoras mecánicas hasta el siglo XX, lo que demuestra la importancia y la durabilidad de su invención.
Máquina analítica de Babbage#
En 1837, el matemático británico Charles Babbage (1791-1871) inició el diseño de la máquina analítica, la cual se muestra en la Fig. 3.

Fig. 3 Máquina analítica de Babbage, expuesta en el Museo de Ciencias de Londres. Imagen compartida a través de Wikimedia Commons.#
Esta máquina estaba diseñada para realizar cálculos matemáticos de manera automática a través de una serie de instrucciones introducidas por medio de un sistema de tarjetas perforadas, el cual estaba basado en el telar de Jacquard, un mecanismo ya utilizado en esa época para controlar equipos mecánicos. Además, su diseño incluía algunos componentes de una computadora moderna, incluyendo una “unidad de memoria” y una “unidad de procesamiento”. La máquina analítica nunca se terminó de construir, debido a limitaciones tecnológicas y financieras.
El trabajo de Babbage se enriqueció con la contribución de la también matemática inglesa Ada Lovelace (1815-1852). Lovelace conoció a Babbage cuando ella tenía 17 años y de inmediato se interesó en la máquina analítica e identificó el potencial que tenía más allá del procesamiento numérico. Percibió que podría usarse para crear cualquier tipo de contenido, incluyendo música y otras formas de arte, anticipando así las capacidades multifuncionales de las computadoras modernas. Lovelace ha sido considerada por algunos como la primera programadora de computadoras de la historia, ya que describió un algoritmo detallado para que la máquina analítica procesara números de Bernoulli. Sin embargo, existe también una controversia sobre el grado de participación de Babbage en la confección de este algoritmo-programa.
Máquina de Turing#
En 1936, el matemático inglés Alan Turing (1912-1954) propuso un dispositivo teórico, conocido en la actualidad como máquina de Turing, que manipula símbolos de una cinta de acuerdo con una tabla de reglas. La máquina de Turing se ilustra en la Fig. 4.

Fig. 4 Representación artística de una máquina de Turing. Imagen de Schadel compartida a través de Wikimedia Commons.#
El cabezal de lectura/escritura lee y escribe símbolos en las celdas de la cinta, de acuerdo con las instrucciones contenidas en la tabla de reglas. La máquina tiene un número finito de estados, incluyendo un estado inicial y uno o más estados finales (o de parada). Las reglas le indican a la máquina qué hacer, según el símbolo que el cabezal lee y el estado actual de la máquina. Por ejemplo, si la máquina está en el estado q1 y lee el símbolo “a”, la máquina podría cambiar al estado q2, escribir un “b” y mover el cabezal a la derecha.
La máquina de Turing simula el funcionamiento de un algoritmo y los conceptos de entrada, procesamiento y salida. Funciona como una base teórica para entender qué puede y qué no puede ser computado, y ha influido en el diseño y teoría de las computadoras y lenguajes de programación modernos.
Computadoras de la II guerra mundial#
Con base en las ideas de Turing, las computadoras Bombe y Colossus fueron construídas durante la II Guerra Mundial (1939-1945) en el Reino Unido, para descifrar mensajes codificados. A pesar de que se consideran de las primeras computadoras digitales electrónicas programables, su programación se realizaba a través de componentes de hardware, como interruptores y enchufes, y no con un programa almacenado.
También durante la II Guerra Mundial, el ejército de Estados Unidos de América construyó ENIAC (Electronic Numerical Integrator and Computer) para calcular tablas de tiro de artillería. Es considerada por algunos como la primera computadora programable digital de propósito general. Era capaz de seguir el modelo de la máquina de Turing, por lo que era Turing-completa. ENIAC se muestra en la Fig. 5.

Fig. 5 ENIAC, siendo programada por Glen Beck y Betty Snyder. Imagen del Ejército de Estados Unidos compartida a través de Wikimedia Commons.#
Arquitectura de von Neumann#
En 1945, el matemático húngaro-estadounidense John von Neumann (1903-1957) propuso un concepto conocido como programa almacenado, en el cual los datos y los programas se almacenan en una estructura llamada memoria, separada de los componentes físicos que ejecutan las instrucciones. Este modelo permite que las computadoras sean más fáciles de reprogramar y es conocido actualmente como arquitectura de von Neumann. La arquitectura de von Neumann se ilustra en la Fig. 6.
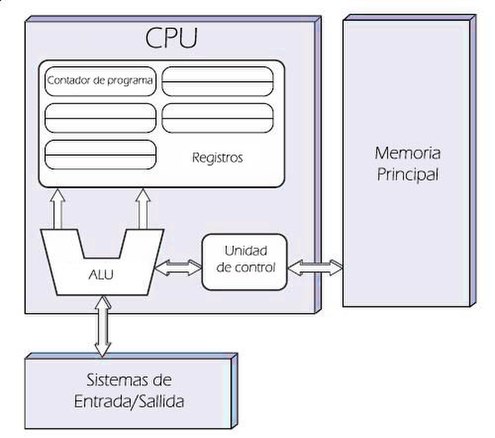
Fig. 6 Diagrama de la arquitectura de von Neumann. Imagen de David Strigoi compartida a través de Wikimedia Commons.#
Componentes de la arquitectura de von Neumann#
Memoria principal#
Almacena las instrucciones de los programas y los datos que utilizan estos programas. Es común denominarla como RAM (Random Access Memory, Memoria de Acceso Aleatorio), lo que significa que toma el mismo tiempo acceder a cualquier posición de la memoria. Cada posición de memoria tiene una dirección a la que se hace referencia cuando se desea leer o escribir.
Unidad Central de Procesamiento#
Tambiénb se le conoce como o CPU (Central Processing Unit). Ejecuta las instrucciones de los programas. Está compuesta por dos partes:
Unidad de Control: determina cuál es la siguiente instrucción a ejecutar. Contiene memorias temporales de alta velocidad y poca capacidad llamadas registros, para almacenar los operandos y el resultado de las instrucciones.
Unidad de Aritmética y Lógica o ALU (Arithmetic and Logic Unit): ejecuta las operaciones aritméticas y lógicas.
Sistemas de entrada y salida#
Permiten que la computadora interactúe con el usuario y, en general, con el mundo exterior. Algunos ejemplos son el teclado y el ratón, como sistemas de entrada, y la pantalla y la impresora, como sistemas de salida.
Código binario#
Las computadoras modernas utilizan circuitos integrados (CI) para procesar y almacenar información en forma de señales eléctricas. Los voltajes bajos y altos representan dos posibles valores de información: 0 y 1. Este es un sistema binario y cada dígito binario (0 o 1) se denomina bit (binary digit).
Los bits se agrupan, por ejemplo, en bytes = 8 bits, para representar elementos de información más complejos, como números más grandes o carácteres de texto. Por ejemplo:
El número decimal
14se representa en binario como1110:
1110=2^3*1 + 2^2*1 + 2^1*1 + 2^0*0=8 + 4 + 2 + 0=14La palabra
bitse representa en código ASCII como:
01100010 01101001 01110100=bit
Lenguajes de programación#
Lenguaje máquina#
El lenguaje máquina es un conjunto de instrucciones binarias (i.e. unos y ceros) interpretables por un CPU. Las instrucciones representan acciones a ser ejecutadas por la computadora. Cada CPU tiene su propio lenguaje máquina.
Un programa consiste de una secuencia de instrucciones en lenguaje máquina.
Por ejemplo, la instrucción de la Fig. 7 suma los contenidos de los registros 1 y 2 y almacena el resultado en el registro 6 de un CPU.

Fig. 7 Instrucción de suma en lenguaje máquina. Ejemplo compartido a través de Wikipedia.#
Lenguajes de alto nivel#
Debido a que programar una computadora en lenguaje máquina es excesivamente lento y complicado, en la década de 1950 comenzaron a crearse lenguajes de programación que, en lugar de unos y ceros, consisten de instrucciones formadas por palabras, usualmente en idioma inglés. A estos lenguajes se les llama lenguajes de programación de alto nivel o simplemente lenguajes de programación.
Existe una gran variedad de lenguajes de programación que han sido creados con diversos fines: científicos, comerciales, educacionales, etc.
Pensamiento computacional#
Las computadoras son ampliamente utilizadas en la actualidad, debido a su capacidad para ayudar a resolver problemas. Sin embargo, el problema expresarse de forma tal que pueda ser implementado en una computadora, mediante un lenguaje de programación, como se ilustra en la Fig. 8.

Fig. 8 Resolución de problemas mediante computadoras.#
El pensamiento computacional es un enfoque para la resolución de problemas basado en conceptos y métodos de las ciencias de la computación. Puede ser aplicado en muchas áreas, no solo en computación. Se considera una de las destrezas fundamentales del siglo XXI.
Conceptos fundamentales del pensamiento computacional#
Descomposición#
Consiste en la división de un problema en subproblemas más pequeños. La idea es que el problema total, de problema de mayor complejidad, se simplifique en problemas más fáciles de resolver.
Ejemplos:
División de un documento en secciones.
Reconocimiento de patrones#
Es la búsqueda de similitudes de un problema a resolver, con problemas ya resueltos.
“Cada patrón describe un problema que ocurre infinidad de veces en nuestro entorno, así como la solución al mismo, de tal modo que podemos utilizar esta solución un millón de veces más adelante sin tener que volver a pensarla otra vez.” (Christopher Alexander, 1977).
Ejemplos:
Abstracción#
Se refiere a la identificación de la información que se necesita y filtrado de la que no se necesita para resolver un problema.
Ejemplos:
Selección de atributos a incluir en una base de datos.
Algoritmos#
Es la descripción, paso por paso, de la solución a un problema.
Ejemplos:
Práctica de programación#
Scratch es un lenguaje de programación orientado a educación. Su nombre proviene de la palabra scratching. Fue desarrollado en 2003 por el MIT Media Lab y es administrado por la Fundación Scratch, una organización sin fines de lucro que lo facilita de manera gratuita. Es software libre distribuido mediante licencia GPLv2.
Considere el paisaje de la Fig. 9.
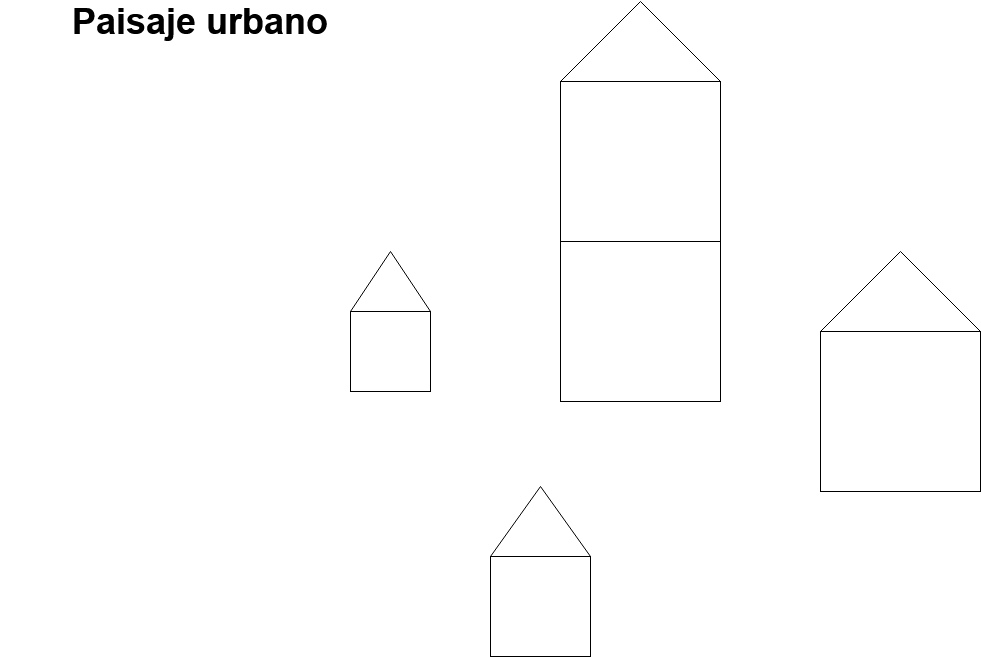
Fig. 9 Paisaje urbano.#
Ingrese al sitio web de Scratch y estudie la intefaz del ambiente de desarrollo. Puede buscar información adicional en otros sitios (ej. Scratch Tutorial for Beginners - Make a Flappy Bird Game, CS50 2021 in HDR - Lecture 0 - Scratch). Revise ejemplos y proyectos de otras personas para saber qué puede hacer con Scratch.
Utilizando los cuatro principios fundamentales del pensamiento computacional, desarrolle un algoritmo para dibujar el paisaje de la diapositiva anterior. Considere las siguientes preguntas orientadoras:
¿Cómo puede dividirse el problema?
¿Qué patrones observa (formas, tamaños, etc.)?
¿Qué información se necesita para hacer los dibujos (ej. medidas)?
¿Qué nivel de detalle requiere el algoritmo?
Implemente en un programa en Scratch el algoritmo que desarrolló.
Algunas sugerencias:
Procure que el código fuente de sus programas sea ordenado y legible.
Reutilice el código fuente mediante bloques, funciones y otros mecanismos.
Use identificadores (ej. nombres de variables, nombres de bloques o funciones) significativos.
Incluya comentarios en el código fuente de sus programas y también escriba documentación externa.
